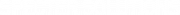When I was reading the MuSig paper from Blockstream I was trying to imagine what would it mean for me as a bitcoin user. Some features of the Schnorr signatures I found really great and convenient, but others are pretty annoying. Here I want to share my thoughts with you, but first, a quick recap:
Elliptic Curve Digital Signature Algorithm
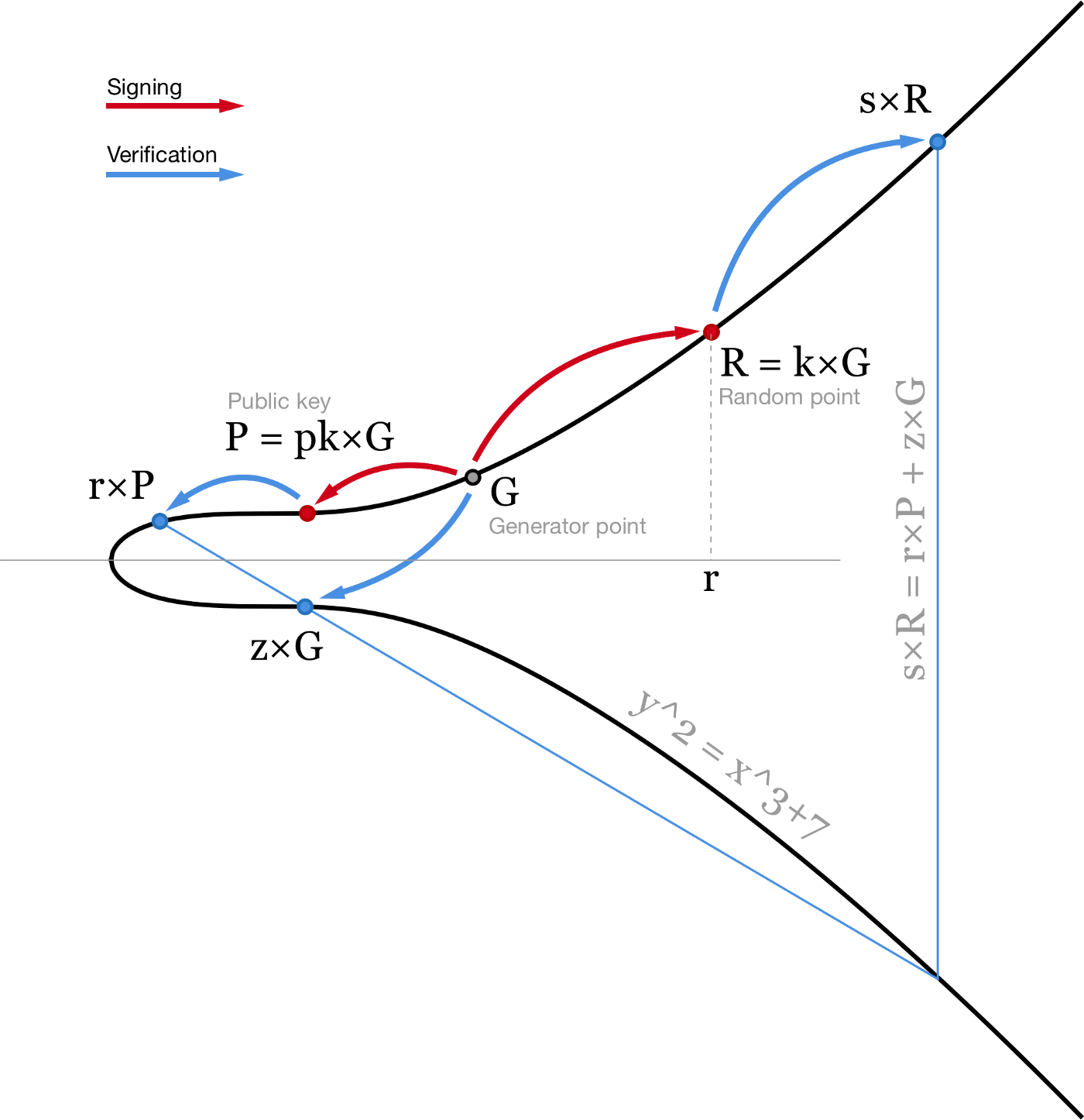
Currently in Bitcoin we use ECDSA. To sign a message m we hash it and treat this hash as a number: z = hash(m). We also need a random or random-looking number k. We prefer not to trust random number generators (too many failures and vulnerabilities are related to bad RGNs) so we usually use RFC6979 to calculate deterministic k based on our secret and the message we are signing.
Using a private key pk we can generate a signature for message m consisting of two numbers: r (x coordinate of the random point R = k×G) and s = (z+r⋅pk)/k. Then, using our public key P = pk×G anyone can verify our signature by checking that point (z/s)×G+(r/s)×P has x coordinate equal to r.
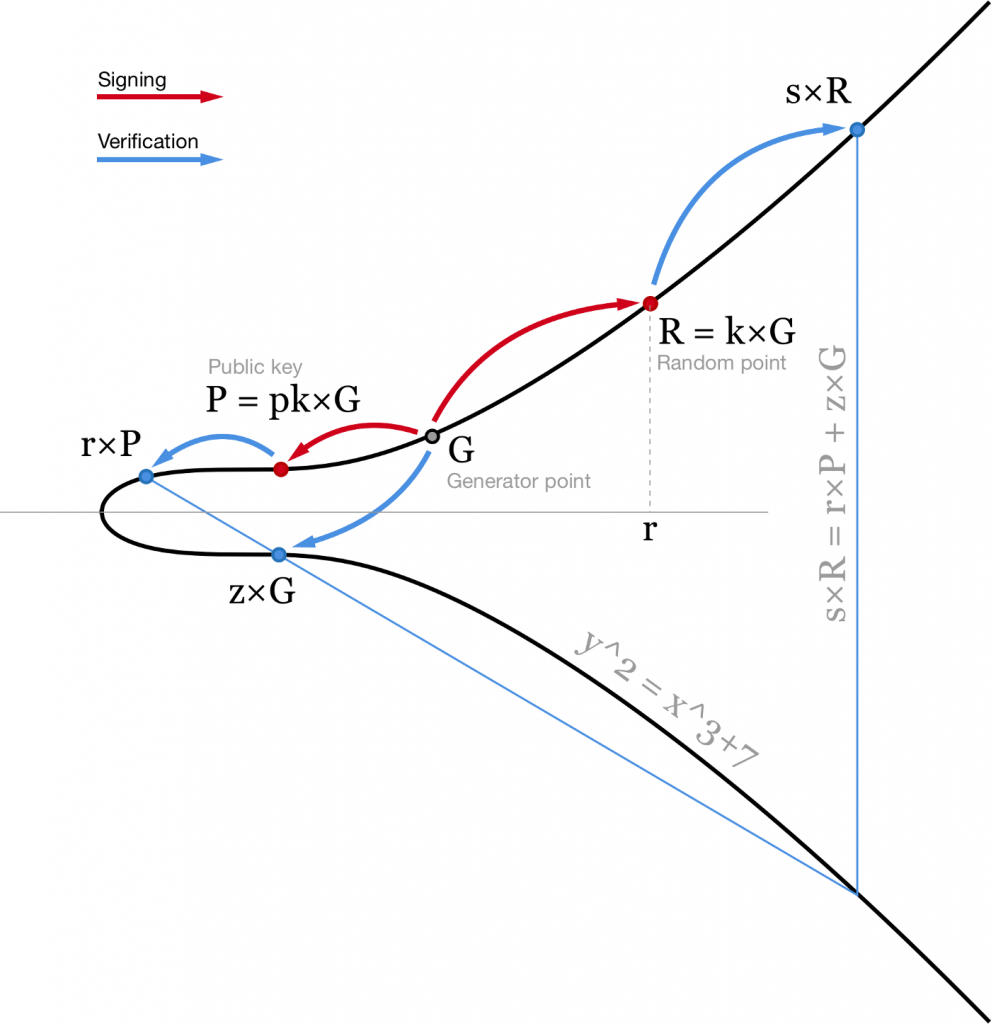 Visualisation of the ECDSA algorithm. Elliptic curve is plotted over real numbers for illustration purposes.
Visualisation of the ECDSA algorithm. Elliptic curve is plotted over real numbers for illustration purposes.
This algorithm is very common and pretty nice but it can be improved. First, signature verification includes inversion (1/s) and two points multiplications and these operations are very computationally heavy. In Bitcoin every node has to verify all the transactions. This means that when you broadcast a transaction, thousands of computers will have to verify your signature. Making verification process simpler will be very beneficial even if signing process is harder.
Second, every node has to verify every signature separately. In case of m-of-n multisig transaction node may even have to verify the same signature several times. For example, transaction with 7-of-11 multisig input will contain 7 signatures and require from 7 to 11 signature verifications on every node in the network. Also such transaction will take a huge amount of space in the block and you will have to pay large fees for that.
Schnorr signatures
Schnorr signatures are generated slightly differently. Instead of two scalars (r,s) we use a point R and a scalar s. Similar to ECDSA, R is a random point on elliptic curve (R = k×G). Second part of the signature is calculated slightly differently: s = k + hash(P,R,m) ⋅ pk. Here pk is your private key, P = pk×G is your public key, m is the message. Then one can verify this signature by checking that s×G = R + hash(P,R,m)×P.
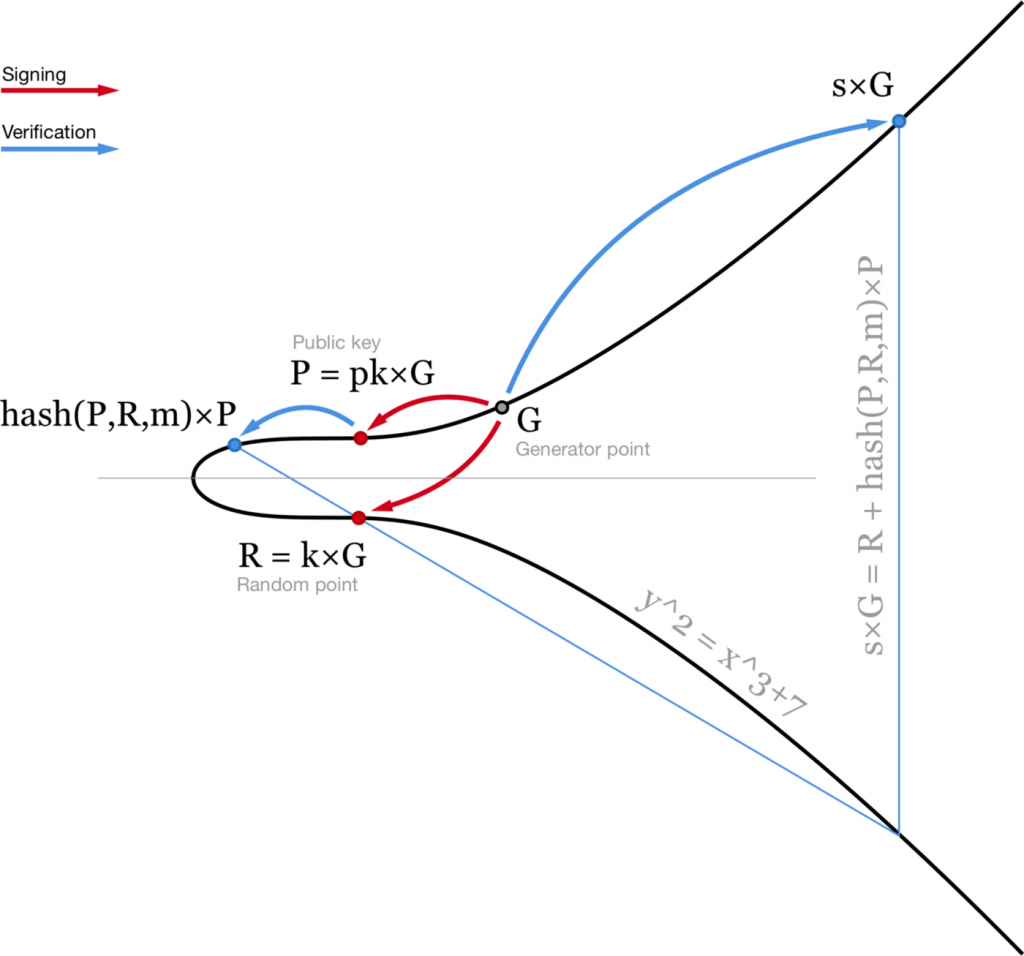 Visualisation of the Schnorr signature verification.
Visualisation of the Schnorr signature verification.
This equation is linear, so equations can be added and subtracted with each other and still stay valid. This brings us to several nice features of Schnorr signatures that we can use.
1. Batch validation
To verify a block in Bitcoin blockchain we need to make sure that all signatures in the block are valid. If one of them is not valid we don’t care which one — we just reject the whole block and that’s it.
With ECDSA every signature has to be verified separately. Meaning that if we have 1000 signatures in the block we will need to compute 1000 inversions and 2000 point multiplications. In total ~3000 heavy operations.
With Schnorr signatures we can add up all the signature verification equations and save some computational power. In total for a block with 1000 transactions we need to verify that:
(s1+s2+…+s1000)×G=(R1+…+R1000)+(hash(P1,R1,m1)×P1+ hash(P2,R2,m2)×P2+…+hash(P1000,R1000,m1000)×P1000)
Here we have a bunch of point additions (almost free in sense of computational power) and 1001 point multiplication. This is already a factor of 3 improvement — we need to compute roughly one heavy operation per signature.
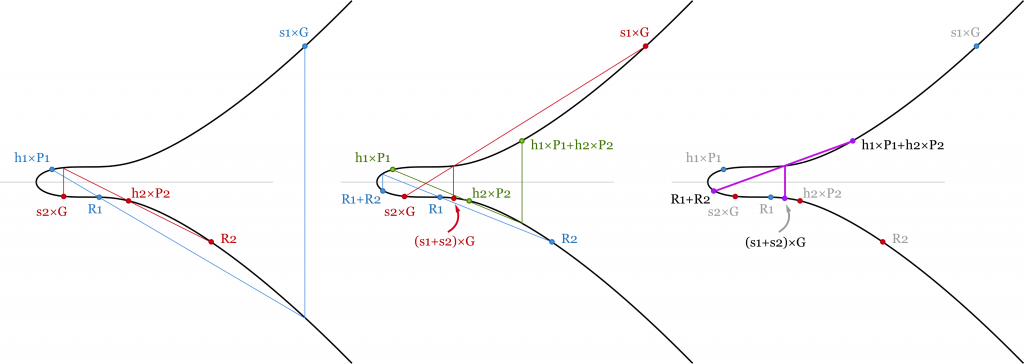 Batch validation of two signatures. As verification equation is linear the sum of several equations is valid as soon as all signatures are valid. We save some computational power as scalar and point additions are much easier than point multiplication.
Batch validation of two signatures. As verification equation is linear the sum of several equations is valid as soon as all signatures are valid. We save some computational power as scalar and point additions are much easier than point multiplication.
2. Key aggregation
We want to keep our bitcoins safe, so we might want to use at least two different private keys to control bitcoins. One we will use on a laptop or a phone and another one — on a hardware wallet / cold wallet. So when one of them is compromised we still have control over our bitcoins.
Currently it is implemented via 2-of-2 multisig script. This requires two separate signatures to be included in the transaction.
With Schnorr signatures we can use a pair of private keys (pk1,pk2) and generate a shared signature corresponding to a shared public key P=P1+P2=pk1×G+pk2×G. To generate this signature we need to choose a random number on every device (k1,k2), generate a random point Ri=ki×G, add them up to calculate a common hash(P,R1+R2,m) and then get s1 and s2 from every device (si = ki + hash(P,R,m) ⋅ pki). Then we can add up these signatures and use a pair (R, s) = (R1+R2, s1+s2) as our signature for shared public key P. Everyone else won’t be able to say if it is an aggregated signature or not — it looks exactly the same as a normal Schnorr signature.
There are three problems with this construction. First one — from UI point of view. To make a transaction we need several communication rounds — to calculate common R, and then — to sign. With two private keys it can be done with a single access to the cold wallet: we prepare an unsigned transaction on our online wallet, choose k1 and write down R1=k1×G together with the unsigned transaction. Then we transfer this data to the cold wallet and sign. As we already have R1 we can sign transaction on the cold wallet in one run. From the cold wallet we get R2 and s2 which we transfer back to the online wallet. Online wallet signs the transaction with previously chosen (k1, R1), combines both signatures and broadcasts a signed transaction. This is pretty much similar to what we have now, but as soon as you add a third private key everything becomes more complicated. Imagine you have a fortune that is controlled by 10 private keys stored in different secure places around the world and you need to make a transaction. Currently you need to go over all these places only once, but if you are using key aggregation you need to do it twice — to assemble all Ri and then to sign. In this case it would probably be better to stay with separate signatures without aggregation — then only one round is necessary.
Post update, thanks to Manu Drijvers for bringing this up: for a provably secure multisignature scheme you need 3 communication rounds:
- Choose a random number ki and corresponding Ri=ki×G and tell everyone only it’s hash ti=hash(Ri), so that everyone can be sure that you will not change your mind after learning other’s random numbers,
- Gather all the numbers Ri together and calculate common R
- Sign
Second problem is a known Rogue key attack. It is nicely described in the paper or here, so I won’t go into details. The idea is that if one of your devices is hacked (say, your online wallet) and pretends that its public key is (P1-P2) then it can control shared funds with its private key pk1. A simple solution is to require a public key to be signed with corresponding private key when we are setting up the devices.
And there is a third important problem. You can’t use deterministic k for signing. There is a simple attack that allows a hacker to get our private key if you are using deterministic k. Attack looks like this: someone hacked our laptop and has a complete control over one of two private keys (say, pk1). We feel safe as our bitcoins require an aggregated signature from both pk1 and pk2. So we are trying to make a transaction as usual, prepare an unsigned transaction and R1 value, transfer them to our hardware wallet and sign there. Then transfer back (R2, s2) and… something happened to our online wallet and it fails to sign and broadcast. We try to do it again, but our hacked computer uses another random value this time — R1′. We sign the same transaction with our hardware wallet again and bring values (R2, s2′) back to our hacked computer. Ups, we’ve lost all our bitcoins.
In this attack hacker gets a pair of valid signatures for the same transaction: (R1, s1, R2, s2) and (R1′, s1′, R2, s2′). Here R2 is the same, but R = R1+R2 and R’=R1’+R2 are different. This means that the hacker can calculate our second private key: s2-s2’=(hash(P,R1+R2,m)-hash(P,R1’+R2,m))⋅pk2 and pk2=(s2-s2′)/(hash(P,R1+R2,m)-hash(P,R1’+R2,m)). I find this the most inconvenient feature of key aggregation — we will need to use a good random number generators everywhere to use key aggregation.
3. MuSig
MuSig solves one of these problem — it makes rogue key attack impossible. The goal is to aggregate signatures and public keys from several parties/devices to a single one but without proving that you have a private key corresponding to the public key.
The aggregated signature corresponds to the aggregated public key. But instead of just adding up public keys of all co-signers we multiply them to some factor. The aggregated public key will be P=hash(L,P1)×P1+…+hash(L,Pn)×Pn. Here L=hash(P1,…,Pn) — a common number depending on all public keys. This nonlinearity prevents attacker from constructing a bad public key like in rogue key attack. Even though the attacker knows exactly what should be his hash(L,Patk)×Patk, he can’t derive Patk from it — it is the same problem as to derive the private key from the public key.
The rest is pretty similar to the previous case. To generate a signature each co-signer choses a random number ki and shares Ri=ki×G with others. Then they add up all these random points to a single R=R1+…+Rn and generate a signature si = ki + hash(P,R,m) ⋅ hash(L,Pi) ⋅ pki. The aggregated signature is (R, s)=(R1+…+Rn, s1+…+sn) and verification equation is the same as before: s×G = R + hash(P,R,m)×P.
4. Merkle Multisig
As you may have noticed, MuSig and key aggregation require all signers to sign a transaction. But what if you want to make a 2-of-3 multisig? Is it possible at all to use signature aggregation in this case, or we will have to use our usual OP_CHECKMULTISIG and separate signatures?
Well, it is possible, but with a small change in the protocol. We can develop a new op-code similar to OP_CHECKMULTISIG that checks if aggregated signature corresponds to a particular item in the Merkle tree of public keys.
For example, if we use a 2-of-3 multisig with public keys P1, P2 and P3, then we need to construct a Merkle tree of aggregated public keys for all combinations we can use: (P1, P2), (P2, P3), (P1, P3) and put the root in the locking script. To spend bitcoins we provide a signature and a proof that our public key is in the tree. For 2-of-3 multisig there are only 3 elements in the tree and the proof will consist of two hashes — the one we want to use and its neighbour. For 7-of-11 multisig there will be already 11!/7!/4!=330 possible key combinations and the proof will require 8 elements. In general the number of elements in the proof scales almost linear with the number of keys in multisig (it’s log2(n!/m!/(n-m)! ).
But with the Merkle tree of public keys we are not limited to m-of-n multisigs. We can make a tree with any public keys we want. For example, if we have a laptop, a phone, a hardware wallet and a recovery seed we can construct a structure that would allow us to spend bitcoins with a laptop and a hardware wallet, a phone and a hardware wallet or just with a recovery seed. This is currently not possible just with OP_CHECKMULTISIG — only if you construct much more complicated script with branches and stuff.
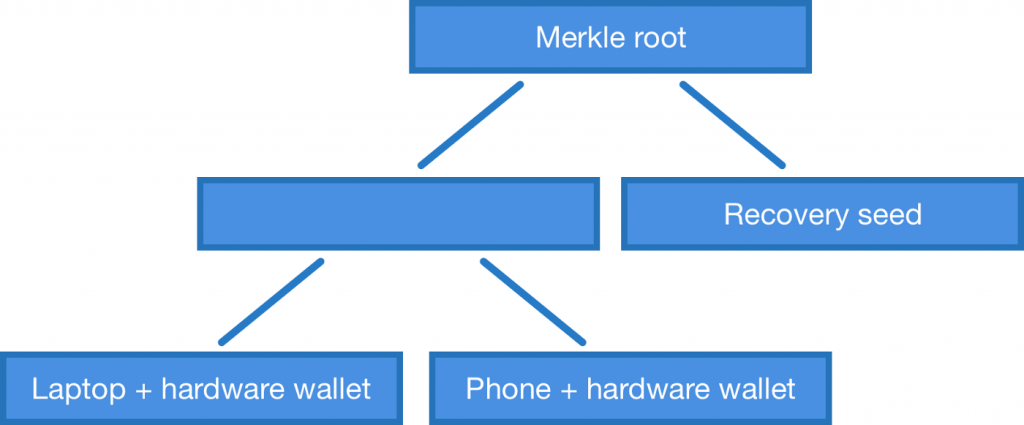 Merkle tree of aggregated public keys. More than just m-of-n multisig.
Merkle tree of aggregated public keys. More than just m-of-n multisig.
Conclusion
Schnorr signatures are great. They can save some computational power during block validation and also give us ability to use key aggregation. The last one has some inconveniences, but we aren’t forced to use them — after all, if we want we can continue using normal multisig schemes with separate, non-aggregated signatures and still gain something. I can’t wait to start using them and I hope they will be included in the Bitcoin protocol soon.
I really liked the paper, the MuSig scheme is smart and the paper itself is very easy to read. I would strongly recommend to look through it if you have time.
P.S. There is also another nice type of signatures — BLS signatures. They look even better than Schnorr in some sense. If you want to know what BLS signatures are about, take a look at my next post.