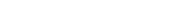In the previous post I wrote about Schnorr signatures and how awesome they are. This one is about Boneh-Lynn-Shacham signatures and their extremely nice features that are not possible with Schnorr.
Shortly, what we know so far:
ECDSA signatures are ok. They do their job and do it well, but nothing more. We can’t combine signatures or keys and every signature has to be verified independently. With multisig transactions, it becomes especially annoying. We have to check all the signatures and the corresponding public keys one by one, waste a lot of space in a block and pay large fees.
Schnorr signatures are awesome — if we do it right we can combine all signatures and public keys in the transaction to a single key and a signature and nobody will find out that they correspond to multiple keys. Also block validation can be faster — we can validate all signatures at once. There are a few issues though:
- Multisig scheme requires several communication rounds. This can be very annoying with cold storage.
- With signature aggregation we have to rely on random number generator — we can’t choose random point R deterministically like we do in ECDSA
- m-of-n multisig scheme is tricky — we need to make a merkle tree of public keys that can get pretty large for large m and n.
- We can‘t combine all signatures in the block to a single signature.
BLS signatures can fix all of the above. We don’t need random numbers at all, all signatures in the block can be combined to a single signature, m-of-n multisig is very simple and we don’t need several communication rounds between signers. In addition to that BLS signatures are 2 times shorter than Schnorr or ECDSA — signature is not a pair, but a single curve point. Sounds amazing! Let’s see how they work.
BLS signatures magic
Before we start we need two new constructions — hashing to the curve and curves pairing.
Hashing to the curve
Normally with ECDSA and Schnorr we hash the message and use this hash in the signing algorithm as a number. For BLS signatures we need a slightly modified hashing algorithm that hashes directly to the elliptic curve. The easiest way is to hash a message as usual and treat the result as an
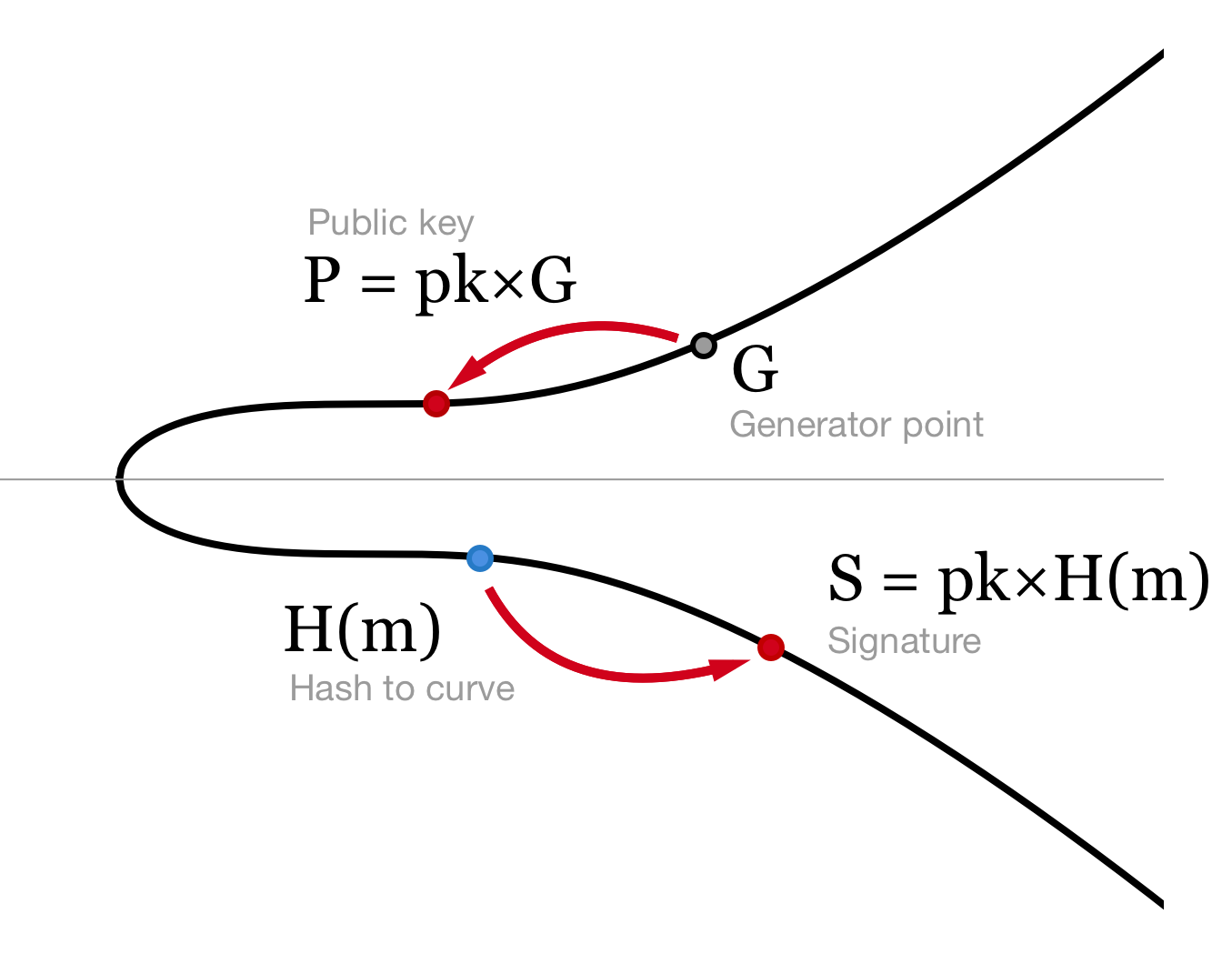
x-coordinate of a point. Elliptic curves (like the one we are using in Bitcoin) usually have about 2²⁵⁶ points and SHA-256 hashing algorithm also gives a 256-bit result. But for every valid x-coordinate there are two points with positive and negative y-coordinate (just because if (x,y) is on the curve y²=x³+ax+b then (x,-y) is also on the curve). This means that our hash has roughly 50% probability to find two points for some x and 50% to find none.
Toy example of hashing to the elliptic curve y²=x³+7 defined over finite field modulo 23. Only half of all x-coordinates have points. Here only third attempt was successful.
To find a point for any message we can try hashing several times by appending a number to the message and incrementing it on fail. If hash(m||0) doesn’t find a point we try hash(m||1), hash(m||2) and so on until we finally get one that matches. Then we choose one of the two corresponding points, say the one with smaller y, and we are done.
Curves pairing
Another thing we need is a very special function that takes two points P and Q on a curve (or on two different curves) and maps them to a number:
e(P, Q) → n.
We also require one important property from this function. If we have some secret number x and two points P and Q we should obtain the same result regardless of which point we multiply by this number:
e(x×P, Q) = e(P, x×Q).
Basically we need to be able to swap multipliers of the points between two arguments without changing the result. More generally all these swaps should give the same result:
e(a×P, b×Q) = e(P, ab×Q) = e(ab×P, Q) = e(P, Q)^(ab)
I am not going to describe how exactly this function works. Underlying math is pretty complicated and if you want to know all the nasty details I would suggest reading this post and references in it. If you want to go deeper — this thesis is completely about pairings. For now we just accept that such functions exist and they don’t reveal any information about our secret number x.
One important note is that we can’t use any elliptic curve here (in particular, standard Bitcoin curve secp256k1 doesn’t work). To make this function efficient and secure we have to use very special curves from “pairing-friendly” family.
BLS signature scheme
Now we have everything we need to construct a BLS signature. As usual our private key is some secret number pk, our public key is P = pk×G and the message we are signing is m.
To calculate the signature we hash our message to the curve H(m) and multiply resulting point by our private key: S = pk×H(m). That’s it! Nothing else — no random numbers, no extra operations, just a hash times the private key! Our signature is just one single point on the curve that takes only 33 bytes in compressed serialisation format!
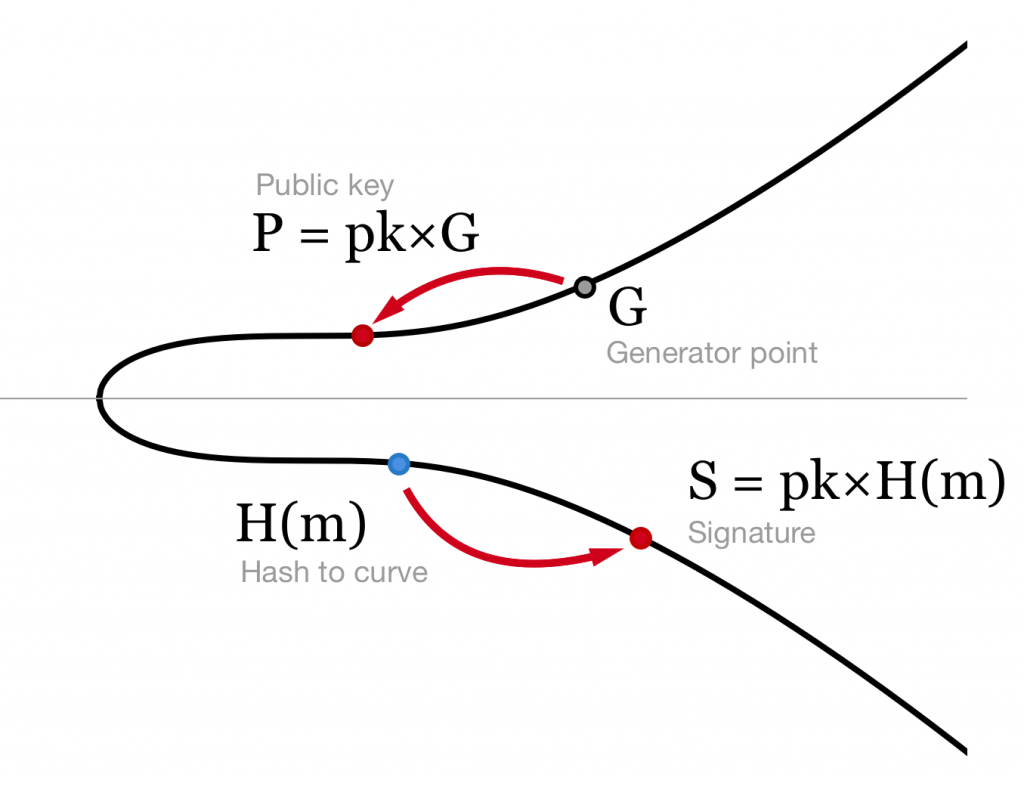BLS signature generation. To obtain signature we multiply a hash of the message by the private key.
To verify this signature one can take our public key P and check that
e(P, H(m)) = e(G, S)
It it true because of the nice property of the pairing function described above:
e(P, H(m)) = e(pk×G, H(m)) = e(G, pk×H(m)) = e(G, S)
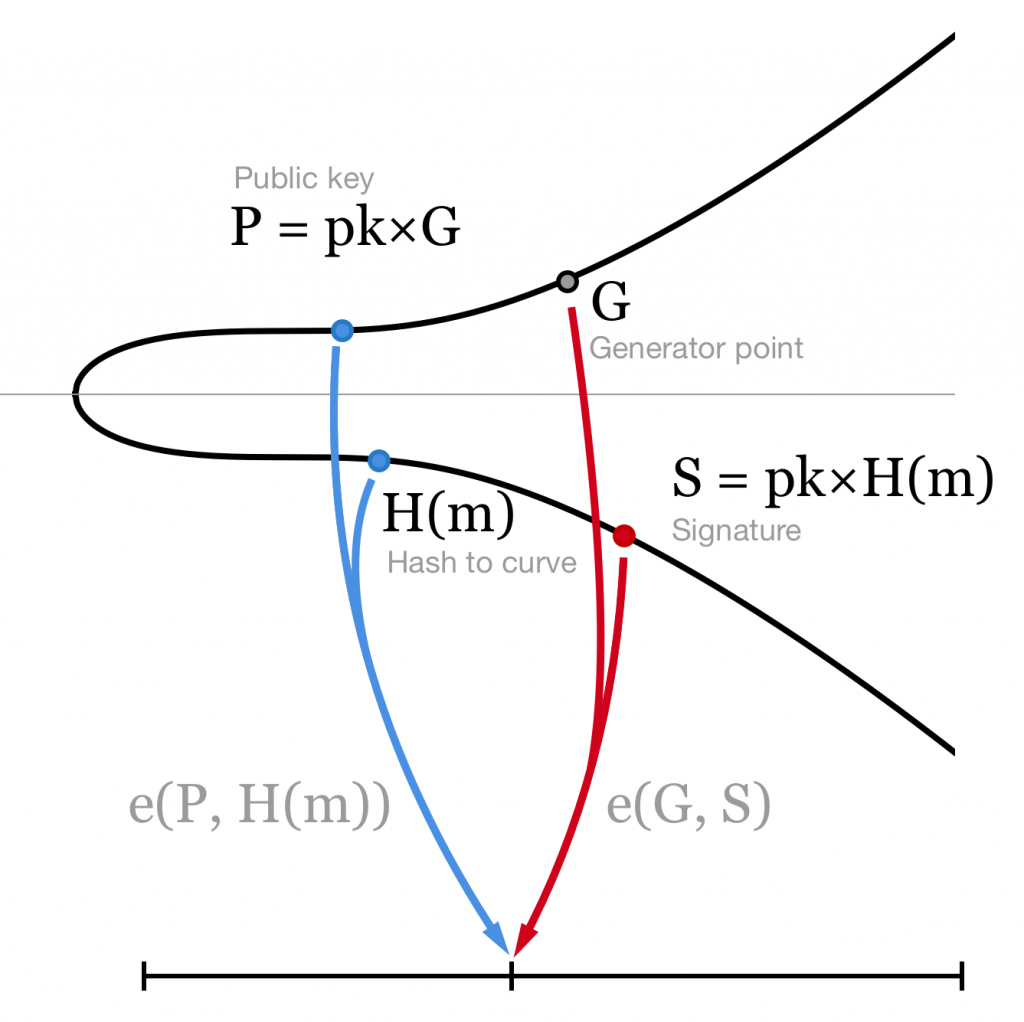BLS signature verification. We just need to check that the public key and the message hash are mapped to the same number as the curve generator point and the signature.
This signature scheme is beautiful and simple, but it also has several very nice features, especially for Bitcoin.
Signature aggregation
Now let’s combine all signatures in the block! Imagine we have a block with 1000 transactions and every transaction contains a signature Si, a public key Pi and a message that is signed mi. Why to store all the signatures if we can combine them? After all, we only care if all signatures in the block are valid. Aggregated signature will be just a sum of all signatures in the block:
S = S1+S2+…+S1000
To verify the block we need to check that the following equality holds:
e(G, S) = e(P1, H(m1))⋅e(P2, H(m2))⋅…⋅e(P1000, H(m1000))
If you look carefully you will see that it’s indeed true:
e(G, S) = e(G, S1+S2+…+S1000) = e(G, S1)⋅e(G, S2)⋅…⋅e(G, S1000) = e(G, pk1×H(m1))⋅…⋅e(G, pk1000×H(m1000)) = e(pk1×G, H(m1))⋅…⋅e(pk1000×G, H(m1000)) = e(P1, H(m1))⋅e(P2, H(m2))⋅…⋅e(P1000, H(m1000))
We still need to know all the public keys and calculate 1001 pairing functions, but at least all the signatures in the block take only 33 bytes. Signature aggregation can be done by a miner and save a lot of space in the block.
Key aggregation and n-of-n multisignature
If we are using multisignature addresses, we are signing the same transaction with different keys. In this case we can do key aggregation like in Schnorr, where we combine all signatures and all keys to a single pair of a key and a signature. Let’s take a common 3-of-3 multisig scheme (it can be done similarly for any number of signers).
A simple way to combine them is to add all the signatures and all the keys together. The result will be a signature S=S1+S2+S3 and a key P=P1+P2+P3. It’s easy to see that the same verification equation still works:
e(G, S) = e(P, H(m))
e(G, S) = e(G, S1+S2+S3) = e(G, (pk1+pk2+pk3)×H(m)) = e((pk1+pk2+pk3)×G, H(m)) = e(P1+P2+P3, H(m)) = e(P, H(m))
Just like in Schnorr we need to protect ourselves from the rogue key attack. We can do it either by asking every co-signer to prove that they have private keys for their public keys (by signing their public keys), or we can add some nonlinearity to the scheme and make rogue key attack impossible. Instead of just summing up all the keys and signatures we multiply them by a certain number and then add:
S = a1×S1+a2×S2+a3×S3
P = a1×P1+a2×P2+a3×P3
Here coefficients of the signatures and keys are calculated deterministically from the public key of the signer and all other public keys:
ai = hash(Pi, {P1,P2,P3})
For example it can be just a concatenation of the signer’s public key and the whole set of public keys used for signing: ai = hash(Pi||P1||P2||P3).
The same verification equation still works. There will be additional coefficients ai in the proof, but the logic remains.
Nice thing about this scheme is that you don’t need several communication rounds between devices. You just need to know who are other signers, and you are all set. This is much simpler than 3-round multisig scheme for Schnorr signatures. It also doesn’t rely on any randomness, it is a completely deterministic signature algorithm.
Subgroup multisignature scheme (m-of-n multisig)
Often we don’t want to use n-of-n multisig scheme, we prefer to use m-of-n, say, 2-of-3. We don’t want to lose all our money just because we’ve lost one of our keys. It would be nice to use key aggregation in this scenario. With Schnorr signatures we were able to do so by using merkle tree of public keys. It is not the most efficient way, but it kinda works. Unfortunately, as soon as you go to high m and n values, merkle tree size blows up exponentially.
With BLS signature scheme there is another method. It’s not that simple though. We will need a normal hash function that outputs a number — hash(x), and a hash to the curve — H(x). We will also need a “setup” phase when we decide to use multisig, but after this we don’t need to communicate anymore — we only need signatures to sign any amount of transactions.
Again I will use a simple example where we want to construct 2-of-3 multisig scheme with keys stored on 3 different devices, but it can be extended to any values of m and n.
Setup phase
Each of our devices has a signer’s number i = 1,2,3 that represent its place in a set, a private key pki and a corresponding public key Pi = pki×G. We calculate an aggregated public key exactly the same way as before:
P = a1×P1+a2×P2+a3×P3, ai = hash(Pi, {P1,P2,P3})
Now every device needs to sign that number i is a member of our aggregated public key (for every i), aggregate these signatures and save the result on corresponding device:
MKi = (a1⋅pk1)×H(P, i)+(a2⋅pk2)×H(P, i)+(a3⋅pk3)×H(P, i)
This signature we will call a “membership key” and we will use it later on for signing. Each membership key is a valid n-of-n signature of the message H(P,i), it means that:
e(G, MKi)=e(P, H(P,i))
Remember this equation, we will need it later. It will be used to prove that we are valid participants of the multisignature scheme.
Signing
Now let’s say we want to sign a transaction only with keys pk1 and pk3. We generate two signatures S1 and S3:
S1 = pk1×H(P, m)+MK1, S3=pk3×H(P, m)+MK3
and add them up to obtain single signature and key:
(S’, P’) = (S1+S3, P1+P3)
I write P’ and S’ here to emphasise that this key and signature are signed only by a subset of signers and it not the same as P that is an aggregated key for all signers. To verify this 2-of-3 signature we need to check that:
e(G, S’) = e(P’, H(P, m))⋅e(P, H(P, 1)+H(P, 3))
We remember that membership keys MK1 and MK3 are valid signatures for messages H(P, 1) and H(P, 3) signed by aggregated key P, so:
e(G, S’) = e(G, S1+S3)=e(G, pk1×H(P, m)+pk3×H(P, m)+MK1+MK3) =e(G, pk1×H(P, m)+pk3×H(P, m))⋅e(G, MK1+MK3)=e(pk1×G+pk3×G, H(P, m))⋅e(P, H(P, 1)+H(P, 3))=e(P’, H(P, m))⋅e(P, H(P, 1)+H(P, 3))
That’s it. A bit more complicated than n-of-n, but still understandable.
Possible implementation
To implement this multisignature scheme we will need to send money to an address corresponding to an aggregated public key P and say that we need at least two signatures. In Bitcoin scripting language locking script could look like this:
OP_2 <P> OP_CHECK_BLS_MULTISIG
Here OP_2 tells that we require two keys to sign the message. We don’t say anywhere that there are 3 signers in total, so one can’t say if it is 2-of-3 or 2-of-100 multisig address. We also don’t reveal this information later.
To spend this output we need to provide a key P’, signature S’ and indexes of participating signers — in our case numbers 1 and 3. Unlocking script could look like this:
OP_1 OP_3 <P’> <S’>
Combining these scripts gives us all necessary information. From OP_1 and OP_3 we know that we need to calculate hashes H(P, 1) and H(P, 3), and then we have everything we need to verify the transaction.
This means that for any m and n we need only:
- one aggregated public key P in the locking script
- one aggregated public key of participating signers P’
- one aggregated signature S’
- m numbers with signer’s indexes.
It is very compact and beautiful!
There is only one thing that I don’t like here… Normally we use addresses only once — we use key derivation like BIP32 to generate new private keys and addresses. But for every new set of private keys we also need a set of new membership keys. One way to do it without running through setup phase every time is to generate a bunch of keys, like 1000 of them and get corresponding membership keys. After all, they are just 32-byte long. Then we will need to run the setup phase again only when all 1000 addresses are used.
Drawbacks
As it was pointed out in the comments here and on twitter, I skipped one important part and made you think that BLS signatures are perfect. They are not. And thanks a lot for bringing this up!
Pairing is hard. I completely skipped that part and we considered that our magic function e(P, Q) is efficient and secure. It is not exactly true.
Paring is not so efficient
BLS signature verification is order of magnitude harder than ECDSA. Signature aggregation for the whole block with 1000 transactions still requires to compute 1000 pairing, so verifying one tiny signature in a block may take longer than verifying 1000 separate ECDSA signatures. The only benefit we achieve here is that we can fit more transactions in the block as aggregated signature takes only ~32 bytes.
Unlike BLS, Schnorr signatures are very efficient — they can be validated all together and this process is factor of 3 more efficient than ECDSA. The question then arises: what is more important for us?
Security proof is harder
Pairing functions are complicated, and it can become our foe if we are not careful enough. On the one hand we want pairing to be efficient to verify signatures faster, on the other hand we don’t want to reveal any information about our secret key. These two requirements fight each other and we need to be extremely careful with our choice of pairing-friendly curves.
There is actually an attack on elliptic curve crypto systems, called MOV attack (named after Menezes, Okamoto, and Vanstone), that allows to reduce security of the system by using our magic pairing function. So we really need to be careful here.
Conclusion
BLS signatures are amazing — we can combine all signatures in a block to a single signature, we can use key aggregation and m-of-n multisig scheme without additional communication rounds, we don’t need to rely on random number generators and the scheme itself looks very nice and simple. There is still room for improvement, standardising and optimising everything will take some time. But I hope at some point this signature algorithm will become good enough to be included in the Bitcoin protocol and we will be able to use all these nice features with smaller and more aggregatable signatures.
I am very excited to see the first author Dan Boneh working on cryptocurrencies. He is a great cryptographer and his coursera crypto course is outstanding. I also recommend his crypto book even though it’s not finished yet. I am sure we will see many interesting schemes and protocol improvements from him and his team in the near future.
